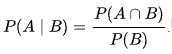- Sep 3, 2011
- 8,107
- 17,661
- AFL Club
- Geelong
Please, what you are saying is purely theoretical (and has nothing to do with objective facts).Some simple statistics to illustrate just how challenging it is to win the flag in any given year. You have to win three finals (if you finish top four) to clinch the premiership. You can lose the first week, so that contingency is eliminated from this analysis. But, whether you win the QF or not, you need three finals wins in succession to lift the cup.
And even if you go into those three finals matches with a supposed win probability of 75% in each game (incredibly high, but let's run with that), your overall probability of winning the three games sits at 0.75 x 0.75 x 0.75 = 0.42.
So even a team who is runaway favourites going into every one of their 'must-win' finals is still well under a 50% chance to get it done in the end. You have to push the win probability in every game to 80% (an utterly ridiculous figure for finals combatants, really) to get the overall probability of a flag to even nudge over 50%.
So the 'flag-flog' dichotomy just isn't supported by any reasonable view of the circumstances at play here. I believe we have the best chance of anyone from here to get it done. But to suggest that any team whose logical probability of success is still 50% (at most) should then absolutely expect to win the whole shebang is just a clear denial of the objective facts at play for mine.
What are the odds of Geelong winning 11 games in a row? Theoretically... based on your statistical premise - the odds of us beating the Saints is something like 5%.
This is true if you look at this as a sequence of games in a row and you look at this from game 1 looking at the future 10 games in a row. However, this week, when we're actually playing the Saints - the odds are not 0.05% are they?
What does that tell you? That outside of theory - we actually don't look at the likelihood of winning as a sequence of games in a row. We judge (objectively) winning/losing chances based on each game on it's own. The Grandfinal and all finals before it will be individual games with specific chances of wining based on each teams form, injuries, illnesses, players available, tactical styles, ground they play at, the weather... essentially new variables.
Back to your example - If a runaway favourite turns up to each game, then it is very likely they will win each game.
Otherwise, you are pretty much saying that Brisbane - assuming they make the top 4 - have just as much chance of winning the premiership as Geelong or Melbourne. And Brisbane will play the MCG in week 1.
Each game we play is a new game. We only look at sequences over a significant proportion of games. But even then, I don't think its applicable to football. It's not like its the same die being spun 100 times. In football, in 100 games, you play 17 other opponents multiple times. Your team will not be the same in game 1 and game 100. You will play in varying grounds with varying weather, tactics, coaches and so on. If it were a perfect predictor, then every team would win a premiership every 18 years.
Last edited: